|
Με την συγκεκριμένη προσομοίωση μπορούμε να μελετήσουμε την απώλεια επαφής δύο σωμάτων σε μια απλή αρμονική ταλάντωση. Έχουμε την δυνατότητα να σύρουμε τα σώματα για να καθορίσουμε το πλάτος της ταλάντωσης. Η μάζα του κάθε σώματος είναι 1kg. Αν ξεπεραστεί η θέση στην οποία χάνεται η επαφή (δηλαδή το φυσικό μήκος του ελατηρίου) δεν έχουμε την δυνατότητα να γυρίσουμε πίσω τον χρόνο. Αν θέλουμε να μην εμφανίζονται τα διανύσματα τοποθετούμε τον δρομέα της κλίμακας των διανυσμάτων στην ακραία αριστερή θέση.
Ας απαντήσουμε πρώτα το ερώτημα «Πότε δυο σώματα βρίσκονται σε επαφή;» και πως μπορούμε το παραπάνω να το περιγράψουμε με εξισώσεις;
Όταν δύο σώματα βρίσκονται σε επαφή τότε το ένα σπρώχνει το άλλο. Η δύναμη που ασκεί το ένα στο άλλο έχει δύο συνιστώσες η μια είναι κάθετη στην επιφάνεια επαφής (κάθετη αντίδραση) και η άλλη είναι παράλληλη στην επιφάνεια επαφής (η οποία ονομάζεται τριβή).
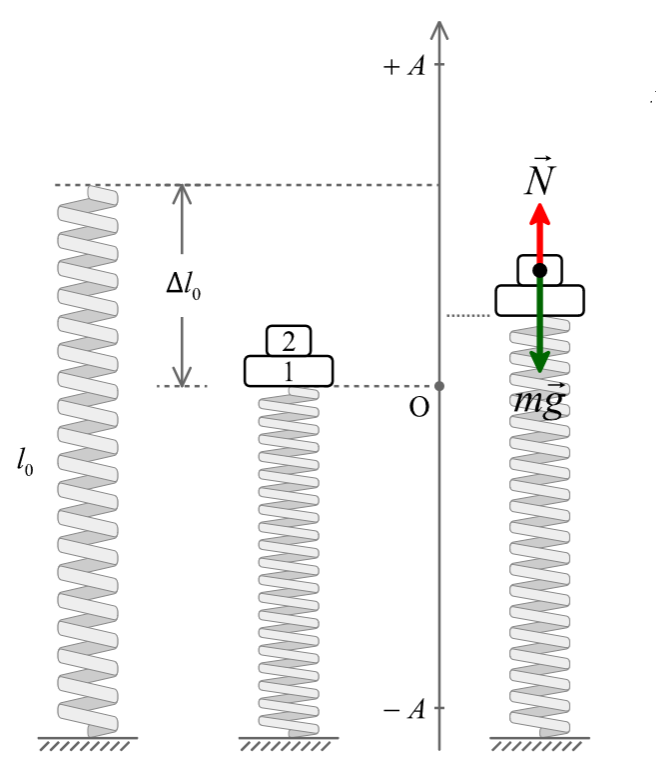
Στο παραπάνω σχήμα έχουμε δύο σώματα: το Σ1 (κάτω σώμα) και το Σ2 (πάνω σώμα). Tο κάτω σώμα σπρώχνει το πάνω με μια δύναμη $N$ και σπρώχνεται από αυτό με μια αντίθετη δύναμη ($\vec{N'}=-\vec{N}$). Αν ασχοληθούμε μόνο με το πάνω σώμα μάζας $m$ τότε οι δυνάμεις που δέχεται είναι η $\vec{N}$ και το $\vec{w}$. Προσανατολίζουμε τον άξονα ώστε να έχει θετική φορά προς τα πάνω (Από το κάτω σώμα προς το πάνω σώμα) τότε η συντεταγμένη (ή αλγεβρική τιμή) $N$ του διανύσματος της δύναμης $\vec{N}$ θα πρέπει να είναι θετική. Αν η $N$ ήταν αρνητική τότε θα έπρεπε να είναι μια ελκτική δύναμη. Τέτοιου είδους δύναμη μπορούμε να έχουμε μόνο αν τα σώματα είναι πχ κολλημένα (καρφωμένα, δεμένα) αλλά όχι όταν είναι απλά σε επαφή. Οπότε :
Όταν δύο σώματα βρίσκονται σε επαφή τότε $N>0$
Για να χρησιμοποιήσουμε την παραπάνω συνθήκη θα πρέπει πρώτα να βρούμε την δύναμη $N$ ως συνάρτηση κάποιων άλλων μεγεθών (στην συγκεκριμένη περίπτωση της απομάκρυνσης). Η δύναμη $N$ δεν έχει εξίσωση ορισμού έτσι υπολογίζεται πάντα έμμεσα από τους νόμους του Νεύτωνα
$$\sum \vec{F}=m\vec{a}$$
$$\vec{N}+\vec{w}=m\vec{a}$$
$$N-mg=ma$$
$$N=mg+ma$$
Όσο υπάρχει επαφή τότε τα σώματα σε κάθε στιγμή έχουν την ίδια ταχύτητα, ίδια επιτάχυνση, ίδια γωνιακή συχνότητα (κλπ όλα τα γεωμετρικά χαρακτηριστικά ίδια) και επειδή κάνουν απλή αρμονική ταλάντωση για το πάνω σώμα έχουμε
$$N=mg+m(-ω^2x)$$
$$N=mg-m\omega^2x$$
Από την παραπάνω εξίσωση φαίνεται πως για αρνητικά $x$ (κάτω από την θέση ισορροπίας) η δύναμη $N$ είναι θετική άρα κάτω από την θέση ισορροπίας το σώμα δεν χάνει ποτέ την επαφή. Ας εφαρμόσουμε την συνθήκη μη απώλειας επαφής
$$N>0$$
$$mg-m\omega^2x>0$$
$$x<\frac{g}{\omega^2}$$
Η τελευταία είναι η συνθήκη που πρέπει να ικανοποιείται ώστε τα δυο σώματα να βρίσκονται σε επαφή.
Ας δούμε λίγο βαθύτερα το παραπάνω αποτέλεσμα
- Επειδή η τελευταία εξίσωση πρέπει να ισχύει για κάθε $x$ αρκεί να ισχύει για
$$A<\frac{g}{ω^2}$$
δηλαδή το μέγιστο πλάτος της ταλάντωσης θα είναι
$$A_\mathrm{max}=\frac{g}{ω^2}$$
Αν το σώμα κάνει ταλάντωση με το παραπάνω πλάτος τότε στο ανώτερο σημείο η δύναμη $N$ θα μηδενιστεί αλλά στην συνέχεια θα συνεχίσει την ταλάντωση μαζί με το δεύτερο.
- Αν πολλαπλασιάσουμε αριθμητή και παρονομαστή με την συνολική μάζα των δύο σωμάτων η ανίσωση $x<\frac{g}{\omega^2}$ γίνεται
$$x<\frac{m_\mathsf{ολ}g}{m_\mathsf{ολ}ω^2}$$
όμως ο παρονομαστής είναι η σταθερά του ελατηρίου επειδή τα δύο σώματα κάνουν ταλάντωση με $D=k=m_\mathsf{ολ}ω^2$
$$x<\frac{m_\mathsf{ολ}g}{k}$$
To δεύτερο μέλος είναι η παραμόρφωση $\Delta l_0$ του ελατηρίου στην θέση ισορροπίας τους συστήματος
|
$$x<\Delta l_0$$ Η απώλεια επαφής συμβαίνει πάντα στο φυσικό μήκος του ελατηρίου |
|
Δηλαδή όσο τα σώματα κάνουν ταλάντωση με πλάτος μικρότερο από την παραμόρφωση του ελατηρίου στη θέση ισορροπίας η επαφή δεν χάνεται. Η επαφή χάνεται στο φυσικό μήκος του ελατηρίου.
Αυτό θα μπορούσε να δειχθεί και ως εξής : Μέχρι να χαθεί η επαφή τα δύο σώματα πηγαίνουν μαζί (έχουν σε κάθε στιγμή την ίδια ταχύτητα και βρίσκονται στην ίδια θέση) άρα θα έχουν και ίσες επιταχύνσεις $\vec{α}_1=\vec{a}_2$. Για το πάνω σώμα ισχύει
$$N-m_2g=m_2a_2$$
Την στιγμή που χάνεται η επαφή ισχύει $N=0$ οπότε
$$m_2a_2=-m_2g$$
$$a_2=-g$$
για το σώμα που είναι δεμένο στο ελατήριο θα ισχύει
$$\sum\vec{F}=m\vec{a}$$
$$F_{\mathsf{ελ}}-m_1g-N=m_1a_1$$
όμως επειδή τα σώματα έχουν την ίδια επιτάχυνση $a_1=a_2=-g$ και $N=0$ οπότε
$$F_{\mathsf{ελ}}-m_1g-0=m_1\left(-g\right)$$
$$F_{\mathsf{ελ}}=0$$
άρα η επαφή χάνεται όταν μηδενίζεται η δύναμη του ελατηρίου και επομένως στην θέση φυσικού μήκους.
- Η συνθήκη $x<\frac{g}{\omega^2}$ γράφεται ως εξής
$$ω^2x<g$$
το αριστερό μέλος της οποίας είναι το μέτρο της επιτάχυνσης όταν το σώμα βρίσκεται στα θετικά του άξονα. Άρα για να μη χάνεται η επαφή θα πρέπει το μέτρο της επιτάχυνσης να είναι μικρότερο από την επιτάχυνση της βαρύτητας. Αυτό το συμπέρασμα είναι αναμενόμενο γιατί αν δεν υπάρχει η δύναμη $N$ τότε η μεγαλύτερη επιτάχυνση (προς τα κάτω) που θα μπορούσε να αποκτήσει το σώμα είναι η επιτάχυνση της βαρύτητας. Αν υπάρχει $N$ τότε η επιτάχυνση του σώματος είναι μικρότερη από $g$ αφού η $N$ έχει κατεύθυνση αντίθετη του βάρους και επομένως η συνισταμένη είναι μικρότερη του βάρους. Αν λοιπόν το κάτω σώμα αποκτήσει επιτάχυνση μεγαλύτερη από $g$ τότε το πάνω δεν μπορεί να ακολουθήσει γιατί το όριο στην επιτάχυνση του είναι το $g$. Για να αποκτούσε επιτάχυνση μεγαλύτερη από $g$ θα έπρεπε κάποιος να τραβήξει το σώμα προς τα κάτω. Τέτοια δύναμη για το κάτω σώμα υπάρχει και είναι του ελατηρίου αλλά δεν υπάρχει για το πάνω. Επομένως η επαφή χάνεται στα θετικά του άξονα και όταν το μέτρο της επιτάχυνσης του κάτω σώματος γίνει μεγαλύτερη από $g$.
|  Φυσική
Φυσική  Ταλαντώσεις και Κύματα
Ταλαντώσεις και Κύματα  Απώλεια Επαφής στην ταλάντωση - HTML5
Απώλεια Επαφής στην ταλάντωση - HTML5 










